Zero-Crossing Detector for Mains Frequency Monitoring
Jeremy Elson, June 2023; updated June 2024
I find it interesting to measure the frequency of the mains power coming out of my wall. Though it’s nominally 60Hz in North America, it varies slightly but continuously, indicating the instantaneous balance between the grid’s power generation and load. These variations can be interesting to watch, for reasons I describe below.
Mains power is 120 volts here, which is not to be trifled with. I wanted a way to safely generate a 3.3 volt square wave that indicates the mains voltage polarity. The low-voltage square wave is easy to feed into counters and timestampers. I’ve seen various solutions for this on the Internet, but all of them seemed a little janky or inconvenient; I wanted to solve the problem properly.
My strategy is to first convert the 120VAC down to a safe 12VAC using an off-the-shelf AC wall wart. I built a circuit board that takes 12VAC from a 5.5mm barrel jack, standard for most wall warts, and emits a 3.3VDC square wave on an SMA jack, useful for plugging into counters. The 12VAC input is both used to power the detector and to provide the signal that’s being measured. The output always reads either ground or 3.3V, depending on the input’s polarity.
Buying Hardware
If you’d like a zero-crossing detector of your own, they’re now available for sale:
A 5-12VAC power adapter with a 2.5mm/5.5mm barrel adapter is required but not included. You might have one in your junk drawer. If not, they’re widely available, for example:
Filtering
The board has two types of hysteresis to keep the output stable and glitch-free. First, there’s a simple low-pass RC filter on the input (components R2 and C4 on the Rev E Schematic) with a cutoff frequency at approximately the mains frequency of 50/60Hz. The comparator, an MCP6561, also has built-in hysteresis. I’ve collected tens of millions of samples without a single glitch.
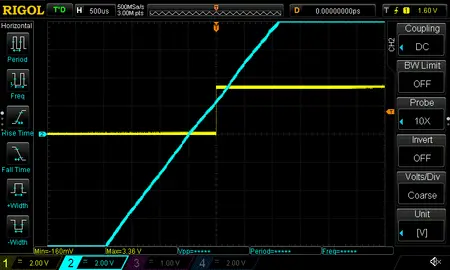
The RC filter phase-shifts the output by about 500\(\mu\)s. If you need more precise phase, depopulate C4 and the output response time will be under 100ns.
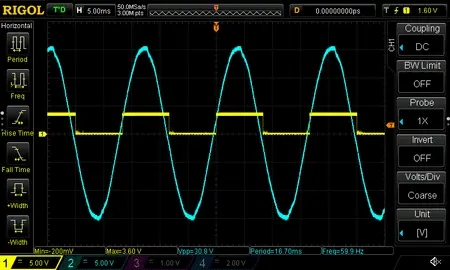
An example waveform is below, along with a zoomed-in view showing the transition. The input is blue; the output is yellow.
Sample Data
I hooked up my zero-crossing detector to an AC wall wart in my Seattle home to measure the grid frequency of the Western Interconnection. The output pulses were measured by a timestamper I made using a microcontroller (an STM32G431) attached to a GPS-disciplined oscillator. The timestamper writes its current clock value to its serial port every time it sees a rising edge from the zero-crossing detector. These timestamps start from an arbitrary epoch—the timestamper’s boot time—but have very good accuracy relative to each other. The timestamper’s resolution is about 6ns, and the GPSDO I use to drive its clock has a frequency accuracy of better than 1E-10 over tau=1s.
The serial data is read by a Python process running on Linux on a Raspberry Pi. The Pi’s system clock is NTP-synchronized to a stratum-0 NTP server in my lab. The serial data reader on the Pi gives each pulse an approximate UTC timestamp. Due to USB and scheduling delays between the timestamper’s output and the RPi Python process, these timestamps have an error of up to about 100ms. Therefore, the frequency indicated is correct to better than 1E-10, but the UTC time at which that frequency occurred could be wrong by up to 100ms.
Three days of data are summarized in the graph below. The graph shows 10-minute averages, but the underlying data, available here, has a timestamp for every AC pulse, over 16.1 million samples. The source code for generating the graphs is available in this Jupyter Notebook.
Use Cases
Why measure the frequency of wall power? Three reasons motivated me: to try to catch a “time error correction” event; to experiment with forensic methods for timestamping audio and video recordings; and for a fun evening of experimentation with another friend on the Western Interconnection.
Time Errors in Grid-Powered Clocks
For over a hundred years, the power grid had a secondary use: to distribute accurate time. More precisely, the 60Hz sine wave that comes out of every power outlet can be used as a stable frequency reference. Henry Ellis Warren was perhaps the first to have this idea; around 1912, he designed a clock called the Telechron that used the mains both to power the clock and as an oscillator. The idea was that once you set the clock to the right time, it would keep good time on its own without having to be set again.
Warren discovered that his early prototypes told time poorly—because the grid itself was not at the proper frequency! His solution was to call the Boston Edison Power Station and ask them to fix their power generation. They were interested in his experimental clock, partially out of profit motive: if the Telechron became popular, they’d sell more electricity to power them. Warren built them a Station Master Clock, which kept a running tally of how far ahead or behind a grid-based clock was from an accurate pendulum clock. Power station operators would adjust the generator frequency to keep the error minimized.
In modern times, the process is more tightly controlled. In the U.S., standards for TEC, or Time Error Correction, are written by NERC, the North American Electricity Reliability Corporation. When the cumulative error of a grid-driven clock exceeds a certain threshold, the grid’s target frequency is changed to run 20 millihertz faster or slower than usual (60.02 or 59.98 Hz) to back out the error.
Integrating the frequency data, we can see how well a grid-referenced clock would have kept time during my measurements:
The phase error varies by several seconds over the course of a few days, an error of about 1e-5. This is roughly the same performance as you’d expect from an ordinary quartz crystal oscillator found in wristwatches. But while a quartz crystal clock will keep gaining or losing time without bound, the magic of a grid clock is that the frequency should be sped up and slowed down to keep the total error within just a few seconds no matter how long the clock is running.
Given my lifelong interest in precise time, I originally built this board so I could see one of these Time Error Corrections in action! Unfortunately, the Western Interconnect seems to have discontinued them. My grid-powered clocks gained about 3 minutes in 6 months during 2023.
For decades, the power grid was perhaps the primary frequency reference for “casual” users, even as other methods of disseminating time and frequency were developed. In the United States, the WWVB radio station started transmitting in 1963, with an estimated 50 million clocks now synchronized by it. The Internet brought the Network Time Protocol, now used to synchronize almost every computer on earth. GPS receivers have also become ubiquitous—though commonly thought of as only providing position information, they also provide fantastically accurate time and frequency. Smartphones are also now in almost everyone’s pockets, which give time synchronized from cell phone towers (which, themselves, typically get time via GPS).
So after nearly a century of providing frequency, U.S. energy regulators proposed in 2009 and 2015 that that Time Error Corrections be discontinued. The reasoning is that TEC is no longer useful due to the ubiquity of other sources of good time, and potentially harmful because it pushes the power grid slightly closer to the threshold at which drastic actions are taken to keep it stable. As NERC wrote in their response to the proposal, “intentionally moving away from a scheduled frequency target of 60 Hertz serves no reliability purpose and effectively ‘wastes’ the safety margins designed into the system by the engineers who planned it.”
Audio and Video Forensics
Another fascinating use of power grid frequency monitoring is a form of forensics called electrical network frequency analysis, which I first learned about from this fascinating video by YouTuber Tom Scott. Imagine you have a video and want to verify exactly what time it was recorded. Audio often picks up the 60Hz hum of nearby electrical lines or equipment. As you can see from the graph at the top, “60 Hz” is actually a frequency that wanders randomly as the balance between supply and demand changes. If you have a video of sufficient length, the changes in frequency form a unique fingerprint that can be matched against a database of known past grid frequencies.
As far as I can tell, there is no public database of such grid frequencies, though various organizations keep private archives. My aspiration (somewhere on my very long to-do list) is to start recording grid frequency long term and make the results available in an easily accessible public database.
A home experiment showing we’re all one grid
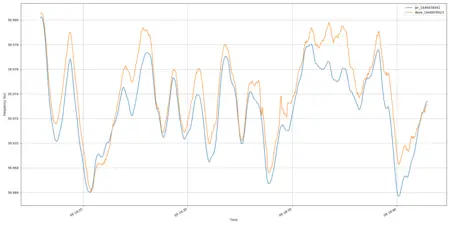
After collecting some initial data, I realized a nice extension would be to compare the data from my home in Seattle to another vantage point elsewhere on the West Coast. I convinced my friend and occasional time-nut Dave, who lives in Berkeley, California, to do a similar experiment. Since Seattle and Berkeley are both part of the Western Interconnection, the frequency data should match. He fed his mains power into a DG1022 signal generator (which has a counter feature) and collected 30 minutes of frequency data. I wrote some software to compare them.
Wow! I was not expecting the two curves to match up so well. What a beautiful result! Of course, since the grid has low impedance, it’s not surprising that the power frequency is synchronized, but it was surprising and delightful to be able to observe this using a simple experiment from home on the first try. It’s like the thrill of launching your own high altitude balloon and taking pictures that show the curvature of the Earth and the dark of space: “of course” the Earth is round and space is dark, but it’s fun and educational to be able to see it for yourself. Overall, it was a fun way to spend an evening.
The main difference between the curves seems to be a constant offset, which is most likely explained by Dave using his counter’s internal crystal oscillator. The difference is about one part in 10^5, which is what you’d expect from a garden-variety crystal.
Schematics and Design Notes
Download: Revision E Schematic [PDF]
The AC input branches branches off to two places: to provide power to the board, and to be conditioned for polarity detection.
The power block is simple: a diode and capacitor rectify the AC input into DC. This feeds into an LDO, the AP7375, which I selected because of its tolerance of inputs up to 45V. (My usual LDO jellybean, the AP7370, only takes up to 18V, which doesn’t leave enough safety margin to the maximum voltage of an unloaded 12V wall wart.)
It was surprisingly hard to build a zero-crossing detector that gives only positive outputs. An op-amp circuit can easily handle positive and negative inputs, but its output also goes rail to rail positive and negative, which is what I was trying to avoid. There are unipolar comparators, but their inputs can’t handle more than a few hundred millivolts below ground. It’s possible to shift an AC signal upwards using something like a diode clamper, but it’s output still goes below ground by a diode-drop, which is too close to the input limit of the unipolar comparators. I could shift the AC input upwards with a capacitive coupler, but that requires I know the input voltage in advance to know how much to bias it; I wanted my circuit to be much less sensitive to the input voltage.
Finally, after consulting with my EE friend Dave, he suggested a nice solution: a direct coupling. That is, my detector uses three resistors (R1, R2, R3) to form a direct-coupled voltage divider such that when the input voltage is -17V, the output is about 0V. When the input is +17, the output is 3.3V. This is fed into a comparator whose threshold is 3.3V/2. The great thing about this is that if the input is smaller in magnitude (e.g., -12V to +12V), the low output goes up and the high output goes down. In other words, as long as the input is centered around zero, the output is always centered around 3.3V/2 (1.65V). This means that even with a fixed comparator threshold of 1.65V, the zero crossing is correctly sensed through a range of input voltages.
The output of the coupler (i.e., at node TP4) can be computed with a system of Kirchhoff equations:
\[\begin{aligned} V_{out} &= R3 (i_1 + i_2) \\ V_{out} &= V_{in} - i_1R2 \\ V_{out} &= 3.3V - i_2R1 \\ \end{aligned}\]I then solved a system of equations with the above equations duplicated twice: once for the high-voltage state and once for the low-voltage state:
\[\begin{aligned} V_{out\_high} &= R3 (i_{1\_high} + i_{2\_high}) \\ V_{out\_high} &= V_{in\_high} - i_{1\_high} R2 \\ V_{out\_high} &= 3.3V - i_{2\_high} R1 \\ V_{out\_low} &= R3 (i_{1\_low} + i_{2\_low}) \\ V_{out\_low} &= V_{in\_low} - i_{1\_low} R2 \\ V_{out\_low} &= 3.3V - i_{2\_low} R1 \\ \end{aligned}\]I then added constraints indicating where I wanted the outputs to be at the high and low voltage inputs. And, finally, set R3 to a fixed value, since otherwise there are infinitely many solutions:
\[\begin{aligned} V_{in\_high} &= +17V \\ V_{out\_high} &= 3.3V \\ V_{in\_low} &= -17V \\ V_{out\_low} &= 0 \\ R3 &= 10000 \end{aligned}\]This solved to
\[\begin{aligned} R1&=8176 \\ R2&=44838 \\ R3&=10000 \\ \end{aligned}\]