Measuring Earth's Circumference with a Ruler
December 2022
One evening I stumbled across this delightful clip from Carl Sagan’s 1980 TV series Cosmos. He describes an ingenious experiment performed by the Greek scholar Eratosthenes who, in the third century B.C.E., estimated the Earth’s circumference within 2% of the modern value. Inspired by this, I decided to replicate the experiment and measure Earth’s circumference for myself!
Eratosthenes was reading manuscripts in the great Library at Alexandria, where he was the Chief Librarian, when he came across a curious fact: in the city of Syene, at exactly noon on the summer solstice, vertical pillars cast no shadow because the Sun is directly overhead. He realized that he could use this observation to compute Earth’s circumference, which until then was not known.
Eratosthenes was lucky here in two ways: first, in that someone had recorded the exact elevation of the Sun in a distant city on a particular day of the year, so he could “synchronize” his own observation by doing it on the same day. (Perhaps the reason the observation was recorded at all was the peculiar nature of it: that the Sun passes directly overhead only on the solstice, because Syene happens to lie near the Tropic of Cancer.) Second, he was lucky because Syene happens to be almost due South of Alexandria, making the calculation more straightforward.
At noon on the next Solstice, Eratosthenes measured the shadow cast by a vertical pillar in Alexandria to be 7° away from vertical. He knew that at the same moment, the Sun was directly overhead in Syene. Assuming that the Sun is so distant from the Earth that its rays are effectively parallel everywhere on its surface, the 7° difference in shadow angle is explained by the Earth’s curvature. Because Alexandria and Syene are on the same meridian, the shadows tell us that Alexandria and Syene are separated by 7° of arc on the Earth’s surface, or about 1/50th of the way around a full 360° circle. He hired professional long-distance walkers who measured the distance from Alexandria to Syene to be 800km. He reasoned that if 1/50th of the way around Earth is 800km, the circumference of the entire Earth must be 800km × 50, or 40,000km. This is remarkably close to today’s estimate of 40,075km.
The beauty of this experiment is its simplicity—simple enough, I realized, that I could repeat it. Though Eratosthenes’ experiment was done on the summer solstice, and with the Sun being directly overhead one of the two observation points, I convinced myself that neither of these things had to be true for the experiment to work. What’s important is measuring the difference between the Sun’s elevation in two places, on any day, at the time when the Sun is highest in the sky.
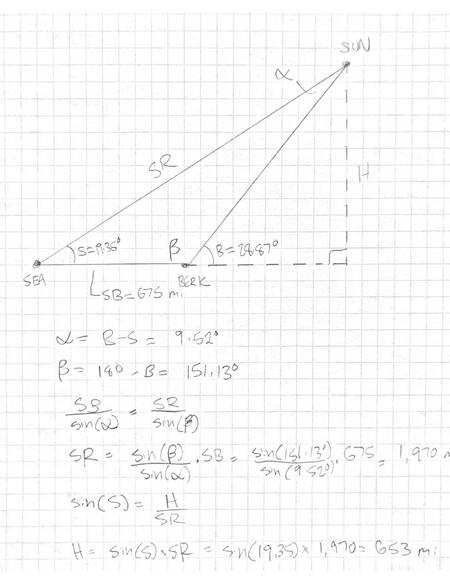
This is where my good friend Dave comes in. Just as Eratosthenes was lucky that Syene was due South of Alexandria, I got lucky having a friend in Berkeley, which is almost due South of Seattle. So, one afternoon in December, at our local solar noon of 12:03pm, we both measured the angle of the Sun’s rays. We measured the height of an object casting a shadow and the length of its shadow along the ground, then computed the arctangent to get the Sun’s elevation. Though the experiment would have worked on any day, doing it so close to the winter solstice made it more accurate: with the noontime Sun so low in the sky, the shadows were long, making measurement errors smaller in comparison.
My setup was just to measure the shadows being cast by window frames in my apartment. My windows face south, so I could do the experiment without even leaving the house.
One disadvantage of winter in Seattle was that 5 minutes later, when it was time to do the measurement, broken clouds had covered the Sun!
I had to wait another couple of minutes for a break in the clouds, then quickly made a chalk mark at the corner of the window-frame shadow. Then I measured the height of the frame corner (42.5”) and the distance to the chalk mark along the floor (121”). This comes out to a Sun elevation of 19.35°.
Meanwhile, Dave was doing a similar measurement in Berkeley: the height of a metal cable running through his deck (12 7/16”) and the distance to its shadow (22 9/16”), giving an elevation of 28.87°.
The difference between our angles was 9.52°. The distance between my house and his is 675 miles according to Google Earth – if you trust Big Cartography. (360°/9.52°) × 675mi is about 25,520 miles, giving us a value with 2.5% error from the real value of 24,902 miles. Not bad!
I blame most of the error on myself: because the sun was only visible for a couple seconds at a time, I didn’t have a chance to measure as precisely as I wanted to. We’ll have to try this experiment again some time on a sunny Seattle day. Still, it was great fun!
What if the Earth is flat?
At the core of this experiment is the assumption that the suns rays are all effectively parallel when they strike Earth because the Sun is so distant compared to Earth’s size. We also assumed that Earth is a sphere, and the observed differences in the Sun’s elevation in different places on Earth is due to Earth’s shape. There is a small but vocal group of people who have a different model: that the Earth is flat, that the Sun is close to its surface, and that the difference in the angle of its rays is due to parallax.
I occasionally watch talks by Flat Earthers, and much of their argument is based on distrust of any fact that they haven’t personally observed. For example, a photo of Earth from space showing its circular profile is not persuasive because NASA is just part of the conspiracy. An account of a short flight between Australia and South Africa is not persuasive because they’ve never been on such a flight, and surely anyone who describes it is lying or was drugged during the trip.
Eratosthenes’ experiment is compelling because it’s something anyone can do without any outside information, or the need to travel to exotic locales. I used information from the Internet only to find the distance from Seattle to Berkeley, but even if we restrict ourselves to personally observable facts, we could still get a decent result by driving the route and using the car’s odometer to estimate the distance.
If a Flat Earther were to do this experiment, it would tell them the height of the Sun above the surface of the Earth, with the help of some geometry: 653 miles. I computed this with basic geometric axioms, seen at the right.
I’m not sure if a Flat Earther would consider that a reasonable distance. What’s completely unreasonable is that the same experiment done in different parts of the world give different results. In Eratosthenes’ experiment, there was an elevation of 90° in Syene and 83° in Alexandria, which would imply a Sun height of over 4,000 miles.
Of course, a much simpler refutation of the Flat Earth model is simply that the sun disappears below the horizon when it sets, and doesn’t set everywhere in the world at once!